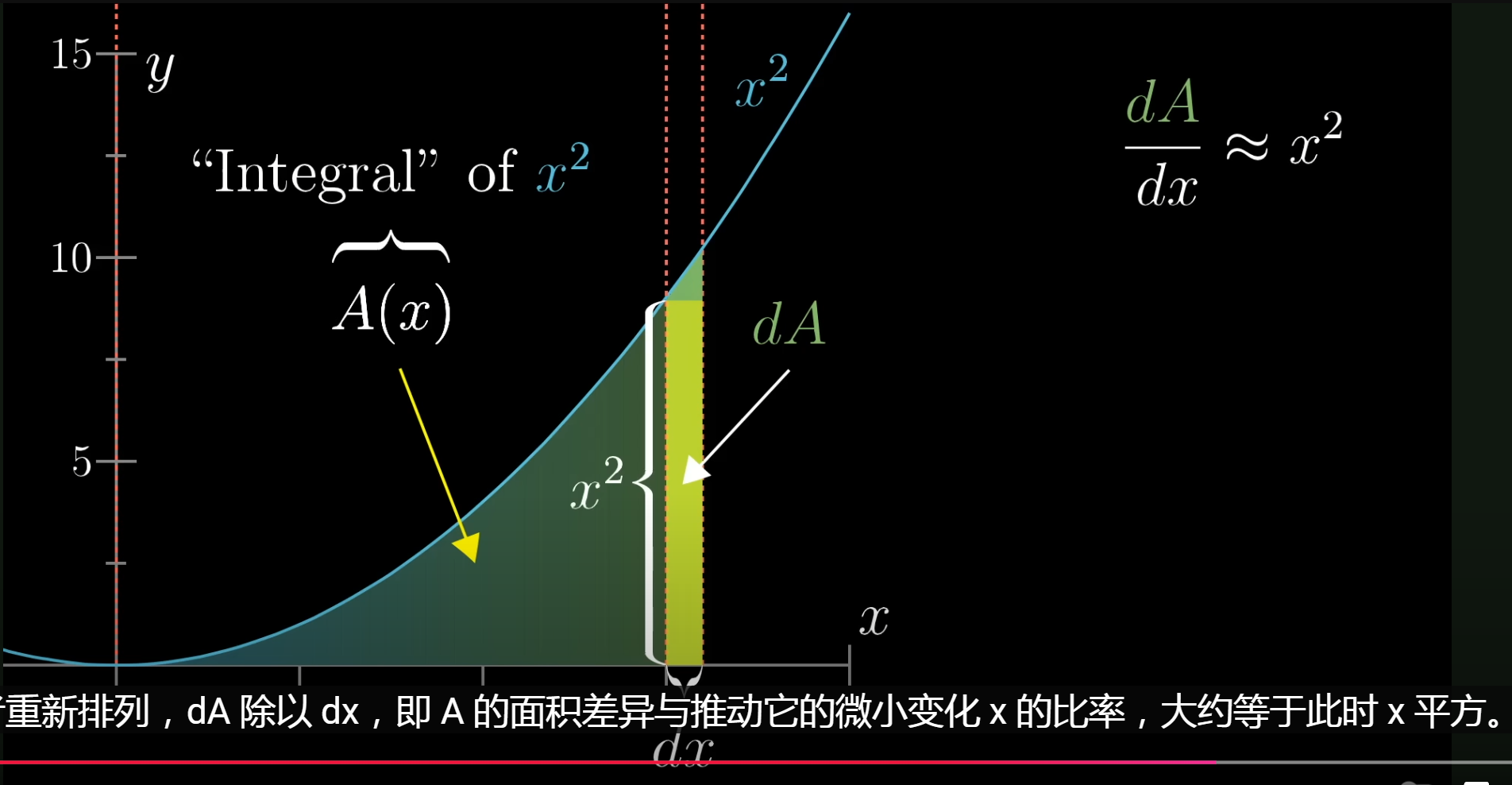
微分与积分可以解决一个经典问题,求曲线下面积。
eg. $f(x) = x^2$
首先需要知道怎么求斜率。
斜率就是描述y对于x的变化。
$slope=\frac{y_1-y}{x_1 – x}$
${x_1 – x}$趋近于无限小,这个值我们用$\Delta x$表示
如果y对于x的变化率用函数 f(x)表示,
那么 $slope = \frac{f(x1) – f(x) } {\Delta x}$
因为$x_1$ 也等于 $x + \Delta x$
所以 $slope = \frac{f(x + \Delta x) -f(x)}{\Delta x}$
这就是斜率公式,也就是导数公式。
那我们用经典曲线函数$x^2$举例,斜率怎么求呢?
代入公式:
$slope=\frac{(x + \Delta x)^2 – x^2}{\Delta x}$
多项式展开:
$slope=\frac{x^2 + 2x\Delta x + \Delta x^2 – x^2} {\Delta x}$
消元 $\Delta x$
$slope=2x + \Delta x$
当$\Delta x$趋近于0时,
$slope=2x$
这就求得了函数$x^2于x点的瞬时斜率$
好,有了斜率下次看看怎么通过积分求面积