2D坐标系中一个点x, y逆时针旋转角度θ后新坐标点x’, y’位置。要用到三角和公式:
cos(Ф+θ) = cosФcosθ – sinФsinθ
sin(Ф+θ) = sinФcosθ + cosФsinθ

由上图,运用三角和公式后,将r·cosФ代入为x, r·sinФ代入为y,就可以通过x, y坐标得出新的x’, y’坐标了:
x’ = xcosθ – ysinθ
y’ = xsinθ + ycosθ
顺时针旋转可以理解为逆时针一个负角度,根据sin(),cos()的奇偶性,即sin(-θ)=-sin(θ),cos(-θ)=cos(θ),可得顺时针旋转的变换公式:
x’ = xcosθ + ysinθ
y’ = ycosθ – xsinθ
另一个问题,三角和公式怎么推导出来。下图用几何法证明了三角和公式的推导:
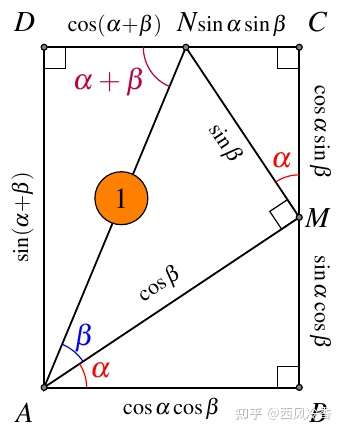
Reference:
平面内直角坐标系中坐标旋转变换公式https://blog.csdn.net/sinat_33425327/article/details/78333946
两角和差的正余弦公式的若干证明方法https://zhuanlan.zhihu.com/p/361839484
https://www.slideserve.com/kirima/chapter-4-2-d-transformations-cartesian-coordinates